第4题
【说明】
0-1背包问题定义为:给定i个物品的价值v[1…i]、小重量w[1...i]和背包容量T,每个物品装到背包里或者不装到背包里。求最优的装包方案,使得所得到的价值最大。
0-1背包问题具有最优子结构性质。定义c[i][T]为最优装包方案所获得的最大价值,则可得到如下所示的递归式。
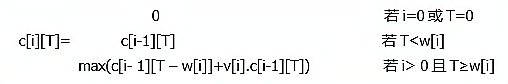
【c代码】
下面是算法的C语言实现。
(1) 常量和变量说明
T: 背包容量
v[]:价值数组
w[]:重量数组
c[][]:c[i][j]表示前i个物品在背包容量为j的情况下最优装包方案所能获得的最大价值
(2) C程序
本人将不方便阅读的图片梳理成文字
0-1背包问题定义为:给定i个物品的价值v[1…i]、小重量w[1...i]和背包容量T,每个物品装到背包里或者不装到背包里。求最优的装包方案,使得所得到的价值最大。
0-1背包问题具有最优子结构性质。定义c[i][T]为最优装包方案所获得的最大价值,则可得到如下所示的递归式。
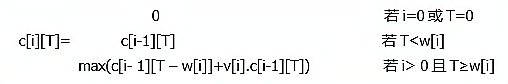
【c代码】
下面是算法的C语言实现。
(1) 常量和变量说明
T: 背包容量
v[]:价值数组
w[]:重量数组
c[][]:c[i][j]表示前i个物品在背包容量为j的情况下最优装包方案所能获得的最大价值
(2) C程序
本人将不方便阅读的图片梳理成文字
#include
#include
#define N6
#define maxT 1000
int c[N][maxT]= {
0
}
;
int Memoized_Knapsack(int v[N],int w[N],int T) {
int i;
int j;
for (i=0; i
for (j=0; j<=T; j++) {
c[i][f]= -1;
}
}
return Calculate_Max_Value(v, w, N-1, T);
}
int Calculate_Max_Value(int v[N],int w[N], int i, int j) {
int temp =0;
if (c[i][j]!=-1) {
(1)
}
if (i==0||j==0) {
c[i][j]=0;
} else {
c[i][j]=Calculate_Max_Value(v, w, i-1, j);
if( (2) ) {
temp=(3) ;
if(c[i][j]
(4)
}
}
}
return c [i][j];
}
问题:4.1
(8分)
根据说明和C代码,填充C代码中的空(1) ~ (4)。
(8分)
根据说明和C代码,填充C代码中的空(1) ~ (4)。
问题:4.2
(4分)
根据说明和C代码,算法采用了 (5) 设计策略。在求解过程中,采用了(6)
(自底向上或者自顶向下)的方式。
(4分)
根据说明和C代码,算法采用了 (5) 设计策略。在求解过程中,采用了(6)
(自底向上或者自顶向下)的方式。
问题:4.3
(3分)
若5项物品的价值数组和重量数组分别为v[]= {0,1,6,18,22,28}和w[]= {0,1,2,5,6,7}背包容量为T= 11,则获得的最大价值为 (7) 。
(3分)
若5项物品的价值数组和重量数组分别为v[]= {0,1,6,18,22,28}和w[]= {0,1,2,5,6,7}背包容量为T= 11,则获得的最大价值为 (7) 。
2019��������� ��������������������������� ������������������������������������ ������������������
正确答案:
你的答案:
请先在App中激活(应用市场搜“软考真题”)
知识点:
试卷:
2019年 下半年 下午试卷 案例
笔记
牛油果果
请先在App中激活(应用市场搜“软考真题”)
2021-05-20
瑾一
请先在App中激活(应用市场搜“软考真题”)
2023-10-31
失之定归
请先在App中激活(应用市场搜“软考真题”)
2020-04-07
曾经的你
请先在App中激活(应用市场搜“软考真题”)
2020-04-04
相见莫相离
请先在App中激活(应用市场搜“软考真题”)
2020-11-06
SUNsHinE
请先在App中激活(应用市场搜“软考真题”)
2021-04-05
落余晖头乍现
请先在App中激活(应用市场搜“软考真题”)
2022-05-24
王老斯
请先在App中激活(应用市场搜“软考真题”)
2022-05-26
Jacen
请先在App中激活(应用市场搜“软考真题”)
2023-08-19
请先在App中激活(应用市场搜“软考真题”)
2020-03-25
牛油果果
请先在App中激活(应用市场搜“软考真题”)
2021-05-20
JsonObject
请先在App中激活(应用市场搜“软考真题”)
2022-10-23
strong
请先在App中激活(应用市场搜“软考真题”)
2023-05-14
王政
请先在App中激活(应用市场搜“软考真题”)
2023-05-18
弯弯
请先在App中激活(应用市场搜“软考真题”)
2024-05-08
有神
请先在App中激活(应用市场搜“软考真题”)
2025-05-12
酸汤肥牛牛
请先在App中激活(应用市场搜“软考真题”)
2025-05-18